Question

The vertex form of the equation of a parabola is y = (x + 3)2 + 53. What is the standard form of the equation? A.y = x2 + 53x + 42 B.y = x2 + 6x + 62 C.y = x2 + 3x + 53 D.y = 6x2 + 9x+ 62

Answer 1

y = (x + 3)² + 53
y = (x + 3)(x + 3) + 53
y = (x(x + 3) + 3(x + 3)) + 53
y = (x(x) + x(3) + 3(x) + 3(3)) + 53
y = (x² + 3x + 3x + 9) + 53
y = (x² + 6x + 9) + 53
y = x² + 6x + 9 + 53
y = x² + 6x + 62

The answer is B.

Answer 2

Option B is correct

`y=x^2+6x + 62`

Explanation:

The standard form for the quadratic equation is given by:

`y = Ax^2+Bx+C`

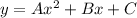
As per the statement:

The vertex form of the equation of a parabola is:

`y = (x + 3)^2 + 53`

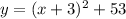
Using the identity rule:

`(a+b)^2 = a^2+b^2+2ab`

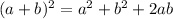
then;

`y = x^2 + 3^2+6x + 53`

⇒
`y = x^2 + 9+6x + 53`

⇒
`y=x^2+6x + 62`

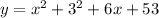
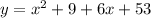
Therefore, the standard form of the equation is;

`y=x^2+6x + 62`