You need to determine an equation that passes through the point (-3,6) and has a slope of m=-5/2
To determine said equation you have to use the point slope form:

Where
m is the slope
(x₁,y₁) are the coordinates of one point of the line.
Replace the formula with the information we have:
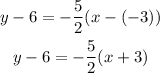
Apply the distributive probability of multiplications to the rigth side of the equation:

Pass the x-related term to the left side and the constant to the rigth side of the equation
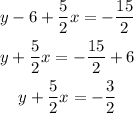
Multiply both sides of the equation by 2 to cancel the denominator of the fractions:
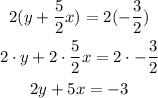
Now reorder the terms to determine the standard form:
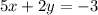
The correct option is B.