step 1
Find the center of the circle
we have that
the center of the circle is the midpoint between the endpoints
sp
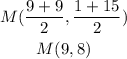
step 2
Find the radius of the circle
we have that
the distance between endpoints is equal to the diameter of circle
so
D=15-1=14 units -------> (difference of the y-coordinates)
Remember that the radius is half the diameter
r=D/2
r=14/2=7 units
step 3
Find the equation of the circle
(x-h)^2+(y-k)^2=r^2
where
*h,k) is the center
r is the radius
substitute
(x-9)^2+(y-8)^2=7^2
(x-9)^2+(y-8)^2=49