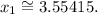Question

Hello how are you? I have a math project and I'm not able to get the solution x if you can help me please!
`x ^(3) - {3x}^(2) - 7 = 0`

Answer 1

We must find the roots of the following cubic polynomial:

`x^3-3x^2-7=0._{}`

---------------

Theory

The roots of the cubic equation:

`x^3+a_1x^2+a_2x^2+a_3=0,`

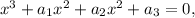
are given by the following formulas:

`\begin{gathered} x_1=S+T-(1)/(3)a_1, \\ x_2=-(1)/(2)(S+T)-(1)/(3)a_1+(1)/(2)i\cdot\sqrt[]{3}\cdot(S-T), \\ x_3=-(1)/(2)(S+T)-(1)/(3)a_1-(1)/(2)i\cdot\sqrt[]{3}\cdot(S-T)\text{.} \end{gathered}`

Where Q, S and T are given by:

`\begin{gathered} Q=(3a_2-a^2_1)/(9), \\ R=(9a_1a_2-27a_3-2a^3_1)/(54), \\ S=\sqrt[3]{R+\sqrt[]{Q^3+R^2}}, \\ T=\sqrt[3]{R-\sqrt[]{Q^3+R^2}}\text{.} \end{gathered}`

The discriminant of the polynomial is:

`D=Q^3+R^2.`

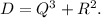
We have the following possibilities:

0. one root is real and two complex conjugates if D > 0,

,

1. all roots are real and at last two are equal if D = 0,

,

2. all roots are real and unequal if D < 0.

---------------

We rewrite the polynomial of the problem in the following way:

`x^3+(-3)\cdot x^2+0\cdot x+(-7)=0._{}`

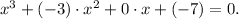
Comparing the last equation with the general case, we identify the coeffients:

`\begin{gathered} a_1=-3, \\ a_2=0, \\ a_3=-7. \end{gathered}`

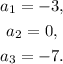
Replacing the values of the coefficients in the formulas of Q and R, we get:

`\begin{gathered} Q=(3\cdot0-(-3)^2)/(9)=-1, \\ R=(9\cdot(-3)\cdot0-27\cdot(-7)-2\cdot(-3)^2)/(54)=(9)/(2). \end{gathered}`

Replacing the values of Q and R in the formula of S and T, we get:

`\begin{gathered} S=\sqrt[3]{((9)/(2))+\sqrt[]{(-1)^3+((9)/(2))^2}}=\sqrt[]{(9)/(2)+\frac{\sqrt[]{77}}{2}}, \\ T=\sqrt[3]{((9)/(2))-\sqrt[]{(-1)^3+((9)/(2))^2}}=\sqrt[]{(9)/(2)-\frac{\sqrt[]{77}}{2}}\text{.} \end{gathered}`

The discriminant of the polynomial is:

`D=Q^3+R^2=(-1)^3+(\frac{\sqrt[]{77}}{2})^2=(73)/(4)>0.^{}`

We have D > 0 so one root is real and two complex conjugates.

We compute only the real root, which is given by:

`\begin{gathered} x_1=S+T-(1)/(3)a_1, \\ x_1=\sqrt[]{(9)/(2)+\frac{\sqrt[]{77}}{2}}+\sqrt[]{(9)/(2)-\frac{\sqrt[]{77}}{2}}-(1)/(3)(-3), \\ x_1=\sqrt[]{(9)/(2)+\frac{\sqrt[]{77}}{2}}+\sqrt[]{(9)/(2)-\frac{\sqrt[]{77}}{2}}+1, \\ x_1\cong3.55415. \end{gathered}`

Answer

The cubic equation has one real root and two complex roots. The real root is:

`x_1\cong3.55415.`