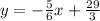First we need to find the line that passes through the points (-5, 1) and (1, -4).
To do so, we can use the linear equation below:

Where m is the slope and b is the y-intercept.
Using the points given, that is, applying the x and y values, we have that:
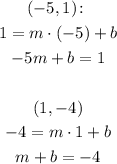
If we subtract the first equation by the second one, we have:
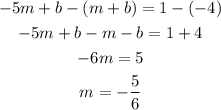
Parallel lines have the same slope, so the slope of the first line is also m = -5/6.
Now, using this slope and the point (8, 3), we can find the equation of the first line:
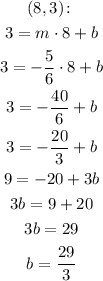
So the equation of the line we want is: