Question

A tetrahedron has four equal triangular faces. The faces of a tetrahedral die are labelled with the numbers one, three, five, and seven. What is the expected value of the random variable representing the numberobserved on a single roll of this die?a. 3b. 3.5C. 4d. 5

Answer 1

The expected value is calculated using the formula:

`E(X)=\sum xP(x)`

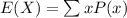
where x represents values of the random variable X and P(x) represents the corresponding probability.

The probability of each number on the face of the tetrahedron being rolled is 1/4. Therefore, the expected value is calculated to be:

`\begin{gathered} E(X)=1((1)/(4))+3((1)/(4))+5((1)/(4))+7((1)/(4)) \\ E(X)=0.25+0.75+1.25+1.75 \\ E(X)=4 \end{gathered}`

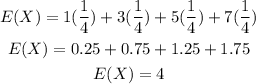
OPTION C is the correct option.