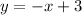Question

Find the equation of the line (in Slope-Intercept form) that goes through the 2 points (6,-3) and (1,2)

Answer 1

The Slope-Intercept form of the equation of a line is:

`y=mx+b`

Where "m" is the slope of the line and and "b" is the y-intercept.

Knowing that the line passes through the points given in the exercise, you can find the slope with the following formula:

`m=(y_2-y_1)/(x_2-x_1)`

You can set up that:

`\begin{gathered} y_2=-3 \\ y_1=2 \\ x_2=6 \\ x_1=1 \end{gathered}`

Then substituting values, you get:

`m=(-3-2)/(6-1)=(-5)/(5)=-1`

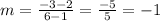
Substitute the slope and the coordinates of one of the points on the line into the equation

`y=mx+b`

And solve for "b":

`\begin{gathered} 2=(-1)(1)+b \\ 2=-1+b \\ 2+1=b \\ b=3 \end{gathered}`

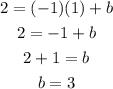
Then, knowing "m" and "b", you can determine that the equation of this line in Slope-Intercept form is:

`y=-x+3`