Answer: The radius of the circle is 40 ft.
Step-by-step explanation
• The square lawn area is 3200 ft².
The formula for the area of a square (A) is:
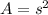
where s represents the side.
If we replace the area, we can find the side:
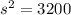
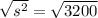
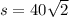
If the sprinkler is placed at the center of the lawn spraying water in a circular pattern that covers the lawn, the diameter ( d ) of the circle is equal to the diagonal of the square:
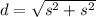
Replacing the values:
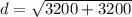
Simpifying:
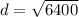
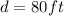
However, as the radius ( r ) is half the diameter then:
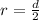
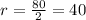
The radius is 40ft.