Question

A square lawn has aroa 3200 ft^2. A sprinkler placed at the center of the lawn sprays water in a circular pattern as shown in the figure. What is the radius of the circle?The radius of the circle is ___ ft.(Simplify your answer. Use a comma to separate answers as needed.)

Answer 1

Answer: The radius of the circle is 40 ft.

Step-by-step explanation

• The square lawn area is 3200 ft².

The formula for the area of a square (A) is:

`A=s^2`

where s represents the side.

If we replace the area, we can find the side:

`s^2=3200`

`√(s^2)=√(3200)`
`s=40√(2)`

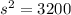
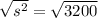
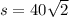
If the sprinkler is placed at the center of the lawn spraying water in a circular pattern that covers the lawn, the diameter ( d ) of the circle is equal to the diagonal of the square:

`d=√(s^2+s^2)`

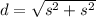
Replacing the values:

`d=√(3200+3200)`

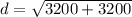
Simpifying:

`d=√(6400)`

`d=80ft`

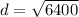
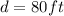
However, as the radius ( r ) is half the diameter then:

`r=(d)/(2)`
`r=(80)/(2)=40`

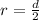
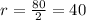
The radius is 40ft.