Question

Simplify each expression, and then arrange them in increasing order based on the coefficient of n^2 .

#Need help ASAP !

Answer 1

increasing order based on coefficient of n^2....

-5(n^3 - n^2 - 1) + n(n^2 - n) <=== this goes in the first box (the top one)
-5n^3 + 5n^2 + 5 + n^3 - 1
-4n^3 + 5n^2 + 4

(n^2 - 1)(n + 2) - n^2(n - 3) <=== this goes in the third box
n^3 + 2n^2 - n - 3 - n^3 + 3n^2
5n^2 - n - 3

n^2(n - 4) + 5n^3 - 6 <=== this goes in the forth box (bottom box)
n^3 - 4n^2 + 5n^3 - 6
6n^3 - 4n^2 - 6

2n(n^2 - 2n - 1) + 3n^2 <=== this goes in second box
2n^3 - 4n^2 - 2n + 3n^2
2n^3 - n^2 - 2n

Answer 2

Explanation:

1. The given expression is:

`-5(n^3-n^2-1)+n(n^2-n)`

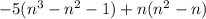
On simplifying, we get

`-5n^3+5n^2+5+n^3-n^2`

`-4n^3+4n^2+5`

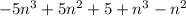
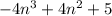
The coefficient of
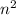`n^2` is 4.

2. The given expression is:

`(n^2-1)(n+2)-n^2(n-3)`

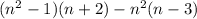
On simplifying, we get

`n^3-n+2n^2-2-n^3+3n^2`

`5n^2-n-2`

The coefficient of
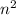`n^2` is 5.

3. The given expression is:

`n^2(n-4)+5n^3-6`

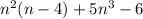
On simplifying, we get

`n^3-4n^2+5n^3-6`

`6n^3-4n^2-6`

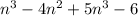
The coefficient of
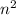`n^2` is -4.

4. The given expression is:

`2n(n^2-2n-1)+3n^2`

`2n^3-4n^2-2n+3n^2`

`2n^3-n^2-2n`

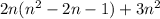
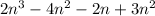
The coefficient of
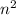`n^2` is -1.

Now, arranging in the increasing order, we have

`n^2(n-4)+5n^3-6`<
`2n(n^2-2n-1)+3n^2`<
`-5(n^3-n^2-1)+n(n^2-n)`<
`(n^2-1)(n+2)-n^2(n-3)`

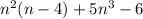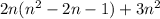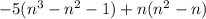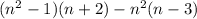
which is the required pattern.