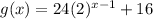Question

Let f(x)=6(2)x−1+4 . The graph of f(x) is stretched vertically by a factor of 4 to form the graph of g(x) . What is the equation of g(x)g(x) ? Enter your answer in the box. g(x) =

Answer 1

Answer: the answer is “24(2)^(x-1)+16” :)

Explanation:

Answer 2

Answer:
`g(x)=24(2)^(x-1)+16`

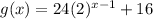
Step-by-step explanation: Given function
`f(x)=6(2)^(x-1)+4`.

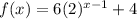We need to find the function that would be stretched vertically by a factor of 4 , that will result function g(x).

According to rules of transformation :

y =C f(x), function f(x) stretched vertically by a factor of C.

According to problem, we need to stretched vertically by a factor of 4.

So, we need to multiply given function f(x) by 4.

On multiplying function by 4, we get

`g(x)=4[6(2)^(x-1)+4]`

On distributing 4 over parenthesis, we get

`g(x)=24(2)^(x-1)+16`

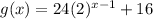
Therefore,

`g(x)=24(2)^(x-1)+16`