2 Answers

Martincho · Answer 1 · 2022-01-31T16:18:43+0000

Answer:

x = 6

Explanation:

Right Triangle

We are given a right triangle whose shortest side has a length of 3 units. This side must be opposite to the smallest acute angle of 30°.

The triangle is shown in the figure attached.

The tangent ratio relates the opposite side with the adjacent side. The formula can be applied to the angle of 30° as follows:

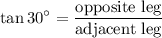
$\displaystyle \tan 30^\circ=\frac{\text{opposite leg}}{\text{adjacent leg}}$

$\displaystyle \tan 30^\circ=(3)/(y)$

Solving for y:

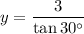
$\displaystyle y=(3)/(\tan 30^\circ)$

Since:

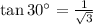
$\tan 30^\circ=(1)/(√(3))$

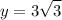
$\displaystyle y=3√(3)$

Now applying the sine to find the hypotenuse x:

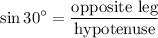
$\displaystyle \sin 30^\circ=\frac{\text{opposite leg}}{\text{hypotenuse}}$

$\displaystyle \sin 30^\circ=(3)/(x)$

Solving for x:

$\displaystyle x=(3)/(\sin 30^\circ)$

Since:

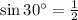
$\sin 30^\circ=(1)/(2)$

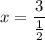
$\displaystyle x=(3)/((1)/(2))$

x = 6

Please log in or register to add a comment.