Answer:
after 0.8411 seconds, the balls are at the same height
Step-by-step explanation:
given the data in the question;
we take a look at the equation which relates the vertical displacement of the object, time elapsed, initial velocity and acceleration of the object;
Δy =
 t +
t +

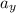 t²
t²
where Δy is the vertical displacement,
 is the initial velocity,
is the initial velocity,
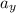 is acceleration of the object and t is time elapsed.
is acceleration of the object and t is time elapsed.
Now let h represent the height above ground level where they meet.
so the distance moved by the falling ball will be;
18 m - h
The ball is moving freely under the influence of gravity.
so
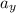 = -g
= -g
Using kinematic relation a freely falling ball
Δy =
 t +
t +

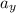 t²
t²
-( 18 m - h ) = 0 -
 gt²
gt²
-18 m + h = -
 gt²
gt²
h = 18 m -
 gt² --------- let this be equ1
gt² --------- let this be equ1
Now lets apply kinematic relation to the raising ball
h = (21.4 m/s)t -
 gt² ----------- let this be equ 2
gt² ----------- let this be equ 2
so equ1 = equ2
18 m -
 gt² = (21.4 m/s)t -
gt² = (21.4 m/s)t -
 gt²
gt²
18 m = (21.4 m/s)t
t = 18 m / 21.4 m/s
t = 0.8411 s
Therefore, after 0.8411 seconds, the balls are at the same height