Question

A crane is being set up on a slope of 7.5°. If the base of the crane is 6.0 feet wide, how many inches should the downhill side of the base be raised in order to level the crane?

Answer 1

9.48 inches

Step-by-step explanation:

From the diagram given, in order to level the crane, it will have to be raised by x units.

Using trigonometric ratios:

`\begin{gathered} tan\theta=\frac{\text{Opposite}}{\text{Adjacent}} \\ \implies\tan 7.5\degree=(x)/(6) \end{gathered}`

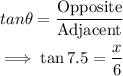
However, since we are required to give our result in inches, convert 6.0 feet to inches.

`\begin{gathered} 1\text{ feet = 12 Inches} \\ 6\text{ feet = 6 }*\text{ 12 =72 Inches} \end{gathered}`

Therefore, we have:

`\tan 7.5\degree=(x)/(72)`

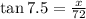
Next, solve for x:

`\begin{gathered} x=72*\tan 7.5\degree \\ x=72*0.1317 \\ x=9.48\text{ inches} \end{gathered}`

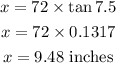
Therefore, the downhill side of the base should be raised by 9.48 inches in order to level the crane.