One way to prove similarity is Side-Angle-Side, or that with an angle which is the same for both triangles and the sides next to it are proportional, the triangles are similar. Starting out with C for our angle, it's clear that it's the same for both sides. Next, a theorem called Power of a Point states that in a situation such as this (there is a point outside of circle, and it has 2 lines going through a circle), CD*CA=CE*CB. We want to reshape this to include the triangles we have (CD & CE, CB & CA), so we can divide both sides by CA and CE to get
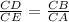
. To prove that the sides are proportional, we can start by looking at the picture - it's clear that we want to prove that angle D is proportional to angle B and angle E is proportional to angle A (angle D clearly does not have the same angle as angle A), so we want CD multiplied by a number, k, to equal CB. Next, we want that same number k multiplied by CE to equal CA to prove that the sides are proportional - a number k is multiplied by all sides to get the side lengths of the other triangles. Therefore, if we assume that CB=CD * k, we want to prove that CE*k=CA, getting

Divide both sides (of the first and last equation) by CD

Multiply both sides by CE and CA
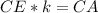
Therefore, as CE*k=CA, CD*k=CB, and ∠C=∠C, the triangles are similar
This was a lot of stuff, so feel free to ask further questions if you're confused on any of this!