Question

What is the oblique asymptote of the function f(x) = the quantity of x squared plus 7 x plus 11, all over x plus 5?

Answer 1

So its basically x^2+7x+11/ x+5

You have to divide the denominator by the numerator. You can use synthetic division or long division.

[-5] . 1 . 7 . 11
--------------------------
x + 2 + 1/x+5

You ignore the remainder, therefore the answer is y = x+2

Answer 2

The quantity is given to be :

`f(x)=(x^2+7x+11)/(x+5)`

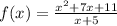
Vertical Asymptote :

For rational function, The vertical asymptote are the points of the singularity of the function in the denominator.

⇒ Find singularities of x + 5

⇒ x + 5 = 0

⇒ x = -5 is the vertical asymptote of the given function f(x)

Horizontal Asymptote :

Now, The numerator's degree = 1 + denominator's degree

So, The vertical asymptote is the equation of the form y = mx + b

Now, divide x² + 7x + 11 by x + 5

We get : x + 2 as quotient and 1 as a remainder

So, y = x + 2 is the horizontal asymptote of the given function f(x).