Question

Three functions are given below: f(x), g(x), and h(x). Explain how to find the axis of symmetry for each function, and rank the functions based on their axis of symmetry (from smallest to largest). f(x) g(x) h(x) f(x) = -2(x − 4)2 + 2 g(x) = 5x2 − 10x + 7 graph of negative 1 times the quantity of x plus 2 squared, plus 2

Answer 1

The axis of symmetry (a.o.s.) can be found in the following ways:
If the vertex is (h, k), then the a.o.s equation is x = h.
If the standard form of
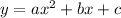
`y=ax^2+bx+c`, then the a.o.s. equation is
`x= (b)/(-2a)`.
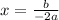
If the x-intercepts
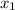
`x_(1)` and
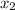
`x_(2)` are given, then the a.o.s equation is
`x= ( x_(1)+ x_(2) )/(2)`

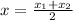
Therefore,
f(x) has a.o.s of x = 4
g(x) has a.o.s of
`x= (-10)/(-2(5))`⇒
`x= 1`
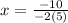
h(x) has a.o.s. of
`x=0` ↔ there are multiple ways to find this

RANKING FUNCTIONS from smallest a.o.s value to greatest: h(x), g(x), f(x)