Question

Given ΔABC, m∠A = 60°, b = 9 and c = 6. Find m∠B. Round to the nearest whole degree

Answer 1

The problem above uses a combination of sine and cosine law of triangle to solve for the m∠B.

Given:
m∠A = 60°, b = 9 and c = 6

Cosine Law:
a^2=b^2+c^2-2bccosA
a^2=(9)^2+(6)^2-2(9)(6)cos(60)
a^2=81+36-54
a^2= 63
a=
`√(63)`

Sine Law

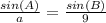
`(sin(A))/(a) = (sin (B))/(9)`
sin B= 9/
`√(63)` sin 60
sin B= 0.98198
B= sin ^-1 (0.98198) = 79.10

Therefore, m∠B is equal to 79.10