Question

What are the real or imaginary solutions of the polynomial equation x^4-52x^2+576?

Answer 1

`x=-6,-4,4,6`.

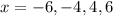Explanation:

We have been given an equation
`x^4-52x^2+576=0`. We are asked to find the real or imaginary solutions of the given equation.

First of all, we will substitute
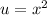`u=x^2` in our given equation as:

`(x^2)^2-52x^2+576=0`

`(u)^2-52u+576=0`

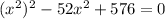
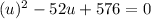
Now, we will solve for u as:

`u^2-36-16u+576=0`

`u(u-36)-16(u-36)=0`

`(u-36)(u-16)=0`

`u-36=0\text{ (or) }u-16=0`

`u=36\text{ (or) }u=16`

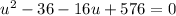
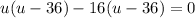
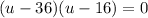
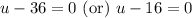
Now, we will undo substitution as:

`x^2=36\text{ (or) }x^2=16`

`x=\pm√(36)\text{ (or) }x=\pm√(16)`

`x=\pm6\text{ (or) }x=\pm\sqrt4`

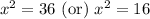
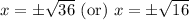
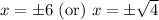
Therefore, the solutions of our given equation are
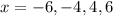`x=-6,-4,4,6`.

Answer 2

the roots of the polynomial for this case will be x1 = 6, x2 = -6, x3 = 4, x4 = -4.You can solve the polynomial using the resolver after making the variable change u = x ^ 2 so that you have a second degree polynomial. Then return the change to find the missing roots. Attached solution.