Question

Which change will quadruple the lateral surface area of a cone?

A) Increase the height and the slant height so that the radius quadruples.
B)Quadruple the height but do not change the radius.
C)Quadruple the radius and the slant height.
D)Increase the height so that the slant height quadruples.

Answer 1

don't know try something else it will probably help

Answer 2

D)Increase the height so that the slant height quadruples.

Explanation:

Given that a cone undergoes changes in height or radius or slant height.

We have to find which change will quadruple the lateral surface area of cone.

Lateral surface area of cone =
`\pi r l`

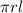
Thus depends on radius and slant height

Let us check one by one options

A) When radius quadruples by increasing slant height we find lateral SA

will change more than quadruples because of change of slant height. Hence wrong.

B) When we quadruple the height 4 times, slant height will not be quadrupled exactly hence option is wrong.

C) If both radius and height are quadrupled then LSA will become 16 times the original hence false.

D) When we increase the height so that slant height quadruples, then radius will be the same, thus making LSA = 4 times the original

Option D is right.