Question

75 Points! ANY CALCULUS GENIUS OUT THERE? PLEASE HELP! Which of the following is the solution to the differential equation dy/dx=x²/y with the initial condition y(3)=-2?

a. y= -2e^(-9+x^3/3)
b. y= 2e^(-9+x^3/3)
c. y = √2x³/3
d. y = √x³/3 - 14
d. y = -√x³/3 - 14

Answer 1

HI there you answer is b

Explanation:

hope this helps

Answer 2

Hey there!

I hope I can help you out!


`(dy)/(dx)= (x^2)/(y)`

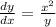
Let's multiply both sides by
`y`


`y(dy)/(dx)=x^(2)`

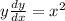
Now, multiply both sides by
`dx`


`y*dy=x^2*dx`

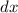
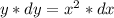
Now, integrate both sides

We get the following equation after integrating


`(y^2)/(2) = (x^3)/(3) +C`

Now, let's solve the value of C by plugging in y= -2 and x=3.

After doing that, you would get the value of C= -7

Now we have this equation:


`(y^2)/(2) = (x^3)/(3) -7`

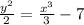
Multiply both sides by 2


`y^2 = (2x^3)/(3) -14`

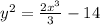
Now, take the square root.


`y = -\sqrt{(2x^3)/(3) -14}`

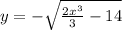
The square root is negative because we want y to have a negative value.

That should be your answer... but there are no matching answer choices.

Hope this helps, though.

Have an awesome day! :)