Question

If f is a continuous function with odd symmetry and limit as x approaches infinity of f of x equals 6, which of the following statements must be true? the limit as x goes to negative infinity of f of x equals negative 6 There are no vertical asymptotes. The lines y = 6 and y = –6 are horizontal asymptotes.

All statements are true.
I only
II only
III only

Answer 1

the function has rotational symmetry about the origin ( since it is odd) and its continuous so there are n vertical asymptotes. There are 2 horizontal asymptoes

Answer is All statements are true.

Answer 2

Answer with explanation:

It is given that, f is a continuous function with odd symmetry.

`y= \lim_(x \to \infty) f(x) =6 \\\\y= \lim_(x \to \infty) f(-x) =6`

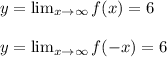
→So, there is no vertical asymptote of the function.

And, →There is one Horizontal Asymptote of function which is equal to, y=6.

Option C:→II only→ There are no vertical asymptotes.