Question

Let y be the difference of two numbers such that one number varies directly as x while the other number varies inversely as x. If y = –7 when x = –2, and y = 5 when x = 1, express y in terms of x. Show your work.

Answer 1

Let a and b the two numbers. So y = a – b. one number varies directly as x , a= k1x. while the other number varies inversely as x, b = k2/x. so the equation y = k1x – k2/x
At y = -7, x =2 then -7 = -2k1 + k2/2
At y = 5, x =1 then 5 = k1 – k2
Solving k1 and k2, 3 and -2 respectively
So y = 3x+2/x

Answer 2

`y=3x+(2)/(x)`

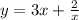
Explanation:

If y is directly proportional to x, then

`y\propto x`

`y=ax`

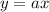
where, a is constant of proportionality.

If y is inversely proportional to x, then

`y\propto (1)/(x)`

`y=(b)/(x)`

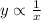
where, b is constant of proportionality.

It is given that y be the difference of two numbers such that one number varies directly as x while the other number varies inversely as x.

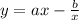`y=ax-(b)/(x)` ..... (1)

We have y=-7 at x=-2.

`-7=a(-2)-(b)/(-2)`

`-7=-2a+(b)/(2)`

`-7=(-4a+b)/(2)`

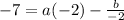
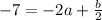
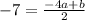
Multiply both sides by 2.

`-14=-4a+b` .... (2)

We have y=5 at x=1.

`5=a(1)-(b)/(1)`

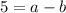`5=a-b` .... (3)

Add equation (2) and (3).

`-14+5=-4a+b+a-b`

`-9=-3a`

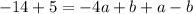
Divide both sides by -3.

`3=a`

The value of a is 3.

Substitute a=3 in equation (3).

`5=3-b`

`5-3=-b`

`2=-b`

`-2=b`

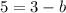
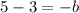
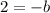
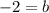
The value of b is -2.

Substitute a=3 and b=-2 in equation (1).

`y=(3)x-((-2))/(x)`

`y=3x+(2)/(x)`

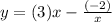
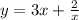
Therefore the required equation is
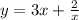`y=3x+(2)/(x)`.