Question

I'm having trouble with this logarithmic equation I will upload a photo

Answer 1

Okay, here we have this:

`\ln \text{ x+}ln(x-4)=\ln (5x)`

Applying the properties of logarithms we obtain:

`\begin{gathered} \ln (x(x-4))=ln(5x) \\ x(x-4)=5x \end{gathered}`
`\begin{gathered} x(x-4)-5x=0 \\ x^2-4x-5x=0 \\ x^2-9x=0 \\ x(x-9)=0 \end{gathered}`

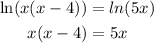
This mean that:

x=0 or x-9=0

x=0 or x=9

We are going to verify which of the solutions works:

x=0:

ln(0)+ln(0-4)=ln(5*0)

ln(0)+ln(-4)=ln(0)

ln(0*-4)=ln(0)

ln(0)=ln(0)

As ln(0)=undefined, the solution x = 0 is false. Let's check the other one: x=9:

ln(9)+ln(9-4)=ln(5*9)

ln(9)+ln(5)=ln(45)

ln(5*9)=ln(45)

ln(45)=ln(45)

This solution satisfies equality, therefore the solution of the equation is x=9.