Question

Determine whether y varies directly with x. If so, find the constant of variation and write the equationX Y1 -23 -65 -10

Answer 1

The Solution:

Given the table of values below:

We are required to determine whether y varies directly with x, find the constant of variation and write out the equation that defines the relationship between x and y

Step 1:

We shall recall the formula for direct variation, which is defined as below:

`\begin{gathered} y\propto x \\ \Rightarrow y=kx\ldots eqn(1) \\ \text{Where k =constant of variation.} \end{gathered}`

Step 2:

We shall apply the initial values of x and y, in order to find the value of k.

`\begin{gathered} \text{When x=1, y=-2} \\ \text{Substituting 1 for x, and -2 for y in eqn(1) above, we get} \\ y=kx \\ -2=k(1) \\ -2=k \\ k=-2 \\ So,\text{ the constant of variation is -2.} \end{gathered}`

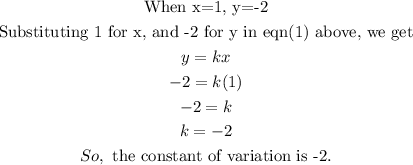
Step 3:

Substitute -2 for k in eqn(1) above.

`y=-2x`

So, the equation connecting x and y is y = -2x

Step 4:

We shall check each pair of values in the table to confirm a direct variation of y with x.

`\begin{gathered} \text{when x=3,} \\ y=-2(3)=-6\text{ ( confirm direct variation)} \\ \text{when x=5} \\ y=-2(5)=-10\text{ (confirm direct variation)} \end{gathered}`

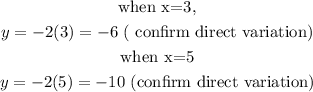
Therefore, it follows that y varies directly with x.