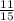Question

If P(A)=2/3, P(B)=4/5, and P(A U B) =11/15, what is P(A ∩ B)?

A) 11/15
B) 13/15
C) 14/15
D) 8/15

Answer 1

the answer is A on apex 

Answer 2

P(A ∩ B) =
`(11)/(15)`

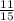
Explanation:

If P(A)=2/3, P(B)=4/5, and P(A U B) =11/15

we need to find out P(A ∩ B)

P(A U B) = P(A) + P(B) - P(A ∩ B)

Now we add P(A ∩ B) on both sides and subtract P(A U B) from both sides

P(A ∩ B) = P(A) + P(B)- P(A U B)

now we plug in the values

P(A ∩ B) =
`(2)/(3) + (4)/(5) - (11)/(15)`

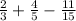
Make the denominators same . LCD is 15

P(A ∩ B) =
`(10)/(15) + (12)/(15) - (11)/(15)`

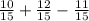
P(A ∩ B) =
`(22)/(15)-(11)/(15)`

P(A ∩ B) =
`(11)/(15)`