Question

A 0.10-kg cart traveling in the positive x direction at 10.0 m/s collides with a 0.30-kg cart at rest. the collision is elastic. what is the velocity of the 0.10-kg cart after the collision?

Answer 1

Explanation :

It is given that,

Mass of cart 1,
`m_1=0.1\ kg`

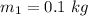
Mass of cart 2,
`m_2=0.3\ kg`

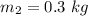
Initial velocity of cart 1,
`u_1=10\ m/s`

Initial velocity of cart 2
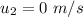`u_2=0\ m/s` ( at rest )

Final velocity of cart 1,
`v_1=?`

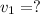
Since, the collision is elastic the momentum will remains conversed.

`m_1u_1+m_2u_2=m_1v_1+m_2v_2`

`0.1* 10+0.3* 0=0.1* v_1+0.3* v_2`

`1=0.1v_1+0.3v_2`

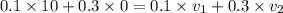
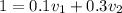
or

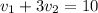`v_1+3v_2=10`............(1)

Now, fr elastic collision the coefficient of restitution is equal to 1. It is given as :

`e=(v_2-v_1)/(u_1-u_2)`

`1=(v_2-v_1)/(u_1-u_2)`

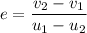
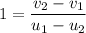
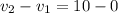`v_2-v_1=10-0`...........(2)

Solving equation (1) and (2) we get:

`v_1=-5\ m/s`

`v_2=5\ m/s`

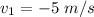
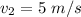
The velocity of the 0.10 kg cart after the collision will be 5 m/s and it is moving in opposite direction or negative x direction.

Hence, this is the required solution.

Answer 2

By definition for an elastic shock, we have that if the second particle is at rest, then the final velocity of the first particle will be given by vf1 = ((m1-m2) * vi1) / (m1 + m2). Then, substituting the values: vf1 = ((0.1-0.3) * 10) / (0.1 + 0.4) = - 5m / s.