Question

Determine the point(s) at which the graph of y^6=y^4-x^4 has a vertical tangent.

Answer 1

Explanation:

We will first find the derivative of the function to get the formula for the slope of the tangent. Using implicit differentiation, we find that:

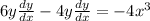`6y(dy)/(dx)-4y(dy)/(dx)=-4x^3` and

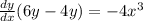`(dy)/(dx)(6y-4y)=-4x^3` Solving for the derivative and at the same time simplifying within the parenthesis:

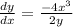`(dy)/(dx)=(-4x^3)/(2y)` so

`(dy)/(dx)=(-2x^3)/(y)`

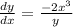
If our tangent line is vetical, that means that the slope is undefined. Our slope is undefined where y = 0. Therefore, we need to find x when y = 0 in our original equation. If y = 0, then

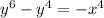`y^6-y^4=-x^4` becomes

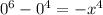`0^6-0^4=-x^4` and

`0 = x^4`

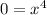
That means that x = 0 (we divide away the negative on the x, and since 0 isn't negative or positive, we get that x^4 = 0)

That means that the point at which the tangent is vertical is (0, 0)