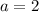Question

Graph the following solution Show the following values: vertical stretch, horizontal stretch, vertical shift and horizontal shift

Answer 1

Given the function:

`f\mleft(x\mright)=2\mleft(x-5\mright)^2-3`

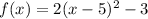
You can identify that it is a parabola because it is a Quadratic Function.

By definition, the Parent Function (the simplest form) of Quadratic Functions, is:

`f(x)=x^2`

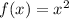
And its graph is:

Notice that its vertex is at the Origin.

-

In this case, you have the Quadratic Function written in Vertex Form:

`f(x)=a(x-h)^2+k`

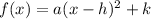
Where "h" is the x-coordinate of the vertex (it indicates the horizontal shift) and "k" is the y-coordinate of the vertex (it indicates the vertical shift). The value of "a" indicates if the parabola is stretched or compressed:

- If:

`|a|<1`

It is compressed.

- If:

`|a|>1`

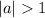
It is stretched.

- If "a" is negative, the parabola opens downward.

- If "a" is positive, the parabola opens upward.

In this case, you can identify that:

`\begin{gathered} a=2 \\ h=5 \\ k=-3 \end{gathered}`

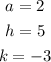
You can find the x-intercepts as follows:

1. Make:

`f(x)=0`

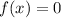
2. Solve for "x".

Then, you get:

`\begin{gathered} 0=2\mleft(x-5\mright)^2-3 \\ \\ (3)/(2)=(x-5)^2 \end{gathered}`
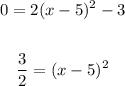
`\begin{gathered} \sqrt[]{(3)/(2)}=\sqrt[]{(x-5)^2} \\ \\ \pm\sqrt[]{(3)/(2)}=x-5 \\ \\ 5\pm\sqrt[]{(3)/(2)}=x\Rightarrow\begin{cases}x_1=5+\sqrt[]{(3)/(2)}\approx6.225 \\ \\ x_2=5-\sqrt[]{(3)/(2)}\approx3.775\end{cases} \end{gathered}`

Knowing all the data, you can graph the parabola.

Hence, the answer is:

- Graph:

- Vertical shift of 3 units down:

`k=-3`

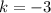
- Horizontal shift of 5 units to the right:

`h=5`

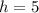
- Vertical stretch by a factor of 2:

`a=2`