Question

Please answer! Explain all steps!

Answer 1

from the grid on Diane's swim you can see that, for every two squares on the grid over the x-axis, it goes up 3 squares over the y-axis, it moves 2 to the right and then 3 up, and you get the next point. What does that mean? well, is a constant speed and thus the graph is a line, with a slope of 3 meters per 2 seconds, so her slope is 3/2 m/s.

now, for Rick's slope, we can just pick two points off of it, say, hmmm 10, 12.5 and 20, 25, and get the slope,




so Diane is doing 3 meters for every 2 seconds, and Rick is doing 5 meters for every 4 seconds.

how long will it be for each to do the 150 meters anyway?


`\bf ~~~~~~~~~~~~~~Diane's\\\\ \begin{array}{ccll} meters&seconds\\ \text{\textemdash\textemdash\textemdash}&\text{\textemdash\textemdash\textemdash}\\ 3&2\\ 150&x \end{array}\implies \cfrac{3}{150}=\cfrac{2}{x}\implies x=\cfrac{150\cdot 2}{3}\implies x=100\\\\ -------------------------------\\\\`


`\bf ~~~~~~~~~~~~~~Rick's\\\\ \begin{array}{ccll} meters&seconds\\ \text{\textemdash\textemdash\textemdash}&\text{\textemdash\textemdash\textemdash}\\ 5&4\\ 150&y \end{array}\implies\cfrac{5}{150}=\cfrac{4}{y}\implies y=\cfrac{150\cdot 4}{5}\implies y=120`

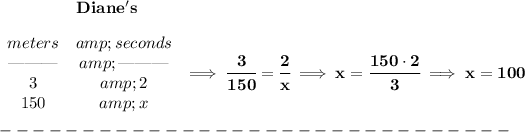
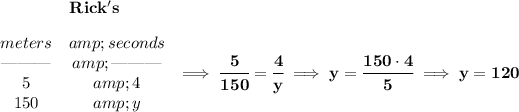
what's their difference? well y - x.

Answer 2

We will be using the formulas:
speed=distance/time
time=distance/speed
distance=speed×time
First let's find out Diane's rate of swimming. We can measure this by finding the slope (y/x) of a given coordinate on the graph. One point is (10,15), so you do 15/10=1.5m/s
Now for Rick's rate of swimming, just take a pair of values from the table. 12.5/10=1.25m/s
By the way m/s is metres per second for this
So at a constant speed of 1.5m/s, Diane swam 150m in 150/1.5= 100 seconds, or 1 minute 40 seconds
And at a constant speed of 1.25m/s, Rick swam 150m in 150/1.25= 120 seconds, or 2 minutes.
So the difference between their two times is 20 seconds