Question

Bruce pulls a spring with a spring constant k=100 Nmk=100\, \dfrac{\text N}{\text m}k=100mN​k, equals, 100, start fraction, start text, N, end text, divided by, start text, m, end text, end fraction, stretching it from its rest length of 0.20 m0.20\,\text m0.20m0, point, 20, start text, m, end text to 0.40 m0.40\,\text m0.40m0, point, 40, start text, m, end text.What is the elastic potential energy stored in the spring?

Answer 1

K_{e} = 2.0 J

Step-by-step explanation:

In this exercise you are asked to calculate the elastic potential energy of a spring

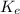`K_(e)` = ½ k x²

where k is the spring constant and x is the displacement from equilibrium position

In this exercise, indicate that the spring constant is k = 100 N/m, the length at rest is x₀ = 20 cm = 0.20 m, up to the position x₁ = 40 cm = 0.40 m, therefore the elongation

Δx = x₁ - x₀

Δx = 0.40 - 0.20

Δx = 0.20 m

let's calculate the elastic potential energy

K_{e} = ½ 100 0.20²

K_{e} = 2.0 J