Question

(b) A car manufacturer claims that its cars are capable of travelling 9 kilometres per litre of fuel. Test runs with 90 cars result in an average distance travelled per litre of fuel of only 8.2 kilometres, with a standard deviation of 2.5 kilometres. Carry out a one tailed test at the 5% level to test the manufacturers claim.

Answer 1

You have the following information:

average = x = 8.2

number of data sample = n = 90

standard deviation = σ = 2.5

In order to test the manufacturers claim, take into account that this situation is about hypothesis test for average value.

First, calculate the Z factor for the normal distribution, given by:

`Z=\frac{\bar{x}-\mu}{\sigma\text{ /}\sqrt[]{n}}`

replace the values of the given parameters into the previous expression:

`\frac{9-8.2}{2.5/\sqrt[]{90}}=3.03`

Next, it is necessary to determine if such value is contained right side of the value of the normal distribution for 5%, which is the same that within an interval of 95% of confidence level.

By searching in a table of the normal distribution for a confidence level of %95. The value is:

`Z=1.65`

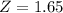
As you can notice, the Z value obtained with the given parameters is greater than the Z value for a 95% confidence level.

Then, you can conclude that the manufacturer statment is false.