Answer:
Option C
The graph of g(x) is the graph of f(x) stretched vertically, flipped over the x-axis and shifted 5 unit down.
Explanation:
Given : The graph
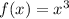 and
and

To find : Which statement best compares the graph of g(x) with the graph of f(x)?
Solution :
Let the parent function be
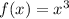
Vertically Stretch:
If y =f(x) , then y = a f(x) gives a vertical stretch if a> 1.
Multiplying the parent function by 4 means you are stretching it vertically,
i,e
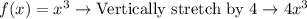
Rotation about x -axis:
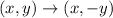
The minus sign means you are rotating it about the x-axis
i,e
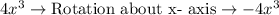
Shifting down : f(x)→f(x)-b
Subtracting 5 means you are moving it down by 5 units
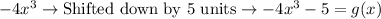
Refer the attached figure below.
Therefore, Option C is correct.
The graph of g(x) is the graph of f(x) stretched vertically, flipped over the x-axis and shifted 5 unit down.