Answer:
Area of octagon = 120.7
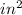
Explanation:
We know that,
Area of a regular octagon =
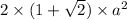 , where a is the length of the side.
, where a is the length of the side.
Now, we have a = 5 inches.
Substituting the value of 'a' in the above formula, we have,
Area of a regular octagon =
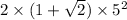
i.e. Area of a regular octagon =

i.e. Area of a regular octagon =
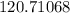
So, we get the area of the octagon is 120.71068
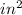 .
.
But, it is required to round the answer to the nearest tenth.
Hence, area of the octagon = 120.7
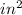 .
.