Question

Information reference tables what is the solution set of the equation log4 (x2 + 3x) − log4 (x + 5) = 1?

a. { }
b. {5}
c. {4, −5}
d. {−4, 5

Answer 1

Use this property of logarithms:


`\log_b\left((x)/(y)\right)=\log_b x-\log_b y`

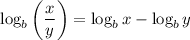
Your equation transforms into:


`log_4\left((x^2+3x)/(x+5)\right)=1`

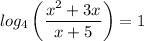
Now, you have to apply the definition of a logarithm to express the equation in exponential form:


`(x^2+3x)/(x+5) = 4^1`

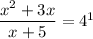
In case you don't remember, this is the definition of a logarithm:


`\log_b x = y \iff b^y = x`

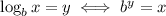
The log is the exponent (y) you have to raise the base (b) to in order to get the power (x).

Finally, solve the rational equation:


`(x^2+3x)/(x+5) =4 \iff x^2+3x=4(x+5)`

`\iff x^2-x-20=0`

`\iff x=(1\pm√((-1)^2-4\cdot(-20)))/(2)= \left \{ {{5} \atop {-4}} \right.`

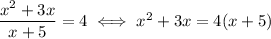
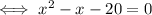
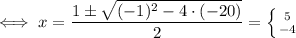
The correct answer is d.