Question

A famous painting was purchased for $490,000 in the year 2021. The value has been increasing at the rate of 4% per year. Calculate the value after 18 years.

Answer 1

Hello there. To solve this question, we'll have to remember some properties about growth.

Say the initial value P of a painting was increasing at a percentage rate r per year for t years. The final value of the painting after that amount of time will be given by the formula:

`P_f=P_i\cdot(1+r)^t`

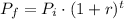
In this case, the percentage must be converted to decimals, dividing it by 100, so in general you may have

`P_f=P_i\cdot\left(1+(r)/(100)\right)^t`

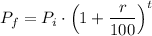
Okay. Now we can solve the question.

We know the initial value of the painting in the year 2021: $490.000

The value has been increasing at the rate of 4% per year. This means that r = 4% and we convert it to decimals in the formula.

We want to calculate its final price after 18 years, that is, when t = 18.

Okay, plugging the values in the formula, we'll get

`\begin{gathered} P_f=490000\cdot\left(1+(4)/(100)\right)^(18) \\ \\ P_f=490000\cdot(1+0.04)^(18) \\ \\ P_f=490000\cdot1.04^(18) \end{gathered}`

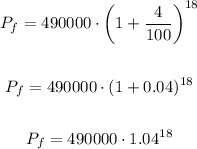
Using a calculator to find an approximation for the power, we'll get

`P_f\approx490000\cdot2.026`

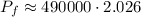
Multiplying the values,

`P_f\approx\$992.740`

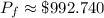
This is the approximate value of this painting in 18 years.