Hello there. To solve this question, we'll have to remember some properties about growth.
Say the initial value P of a painting was increasing at a percentage rate r per year for t years. The final value of the painting after that amount of time will be given by the formula:
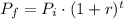
In this case, the percentage must be converted to decimals, dividing it by 100, so in general you may have
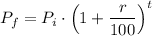
Okay. Now we can solve the question.
We know the initial value of the painting in the year 2021: $490.000
The value has been increasing at the rate of 4% per year. This means that r = 4% and we convert it to decimals in the formula.
We want to calculate its final price after 18 years, that is, when t = 18.
Okay, plugging the values in the formula, we'll get
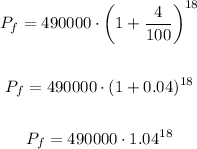
Using a calculator to find an approximation for the power, we'll get
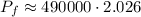
Multiplying the values,
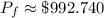
This is the approximate value of this painting in 18 years.