Question

Instructions:Select the correct answer from each drop-down menu.

The equation of the graphed line in slope-point form using the point (2, -1) is ________

a)
`y+1=4x-8`
b)
`y+1= (1)/(4)(x-2)`

and its equation in slope-intercept form is _________

a)
`y= (x)/(4)- (3)/(2)`
b)
`4y=x-6`

Answer 1

The equation of the graphed line in slope-point form using the point (2, -1) is
b)
`y+1= (1)/(4)(x-2)`

and its equation in slope-intercept form is _________
a)
`y= (x)/(4)- (3)/(2)`

Answer 2

(1)
`y+1=(1)/(4)(x-2)`

(2)
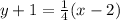
`y=(x)/(4)-(3)/(2)`

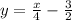
Explanation:

From the given graph it is clear that the line passes through two point (-2,-2) and (2,-1). So, the slope of the line is

`Slope=(y_2-y_1)/(x_2-x_1)`

`Slope=(-1-(-2))/(2-(-2))`

`Slope=(1)/(4)`

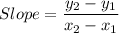
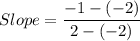
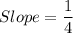
Slope of the given line is 1/4.

Point slope form of a line is

`y-y_1=m(x-x_1)`

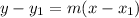
where, m is the slope.

The slope of the line is 1/4 and it passes through the point (2,-1), So, the point slope form of the given line is

`y-(-1)=(1)/(4)(x-2)`

`y+1=(1)/(4)(x-2)`

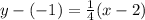
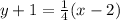
The point slope form of the given line is
`y+1=(1)/(4)(x-2)`.

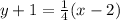The point slope form of a line is

`y=mx+b`

where, m is slope and b is y-intercept.

Simplify the above equation to find the slope intercept form of given line is

`y+1=(1)/(4)(x)+(1)/(4)(-2)`

`y+1=(x)/(4)-(1)/(2)`

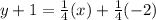
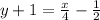
Subtract 1 from both sides.

`y+1-1=(x)/(4)-(1)/(2)-1`

`y=(x)/(4)-(3)/(2)`

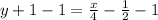
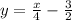
Therefore, the slope intercept form of the given line is
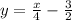`y=(x)/(4)-(3)/(2)`.