Question

A horizontal pipe of diameter 0.768 m has asmooth constriction to a section of diameter0.4608 m . The density of oil flowing in thepipe is 821 kg/m3. If the pressure in the pipe is 7120 N/m^2 and in the constricted section is 5340 N/m2, what is the rate at which oil is flowing?Answer in units of m^3/s

Answer 1

The diameter of the pipe is d = 0.768 m

The diameter of smooth constriction is d' = 0.4608 m

The density of oil is

`\rho\text{ = 821 }(kg)/(m^3)`

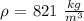
The pressure in the pipe is, P = 7120 N/m^2

The pressure in the constricted section is P' = 5340 N/m^2

We have to find the rate of the flowing.

The area of the pipe will be

`\begin{gathered} a=\pi\text{ (}(d)/(2))^2 \\ =\text{ 3.14}*((0.768)/(2))^2 \\ =0.463m^2 \end{gathered}`

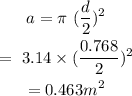
The area of the constricted section will be

`\begin{gathered} a^(\prime)=\text{ }\pi*((d^(\prime))/(2))^2 \\ =3.14*((0.4608)/(2))^2 \\ =0.1667m^2 \end{gathered}`

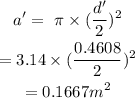
The formula to find the rate of flow is

`V=\text{ aa'}\sqrt[]{(2(P-P^(\prime)))/(\rho(a^2-a^(\prime2)))}`

Substituting the values, the rate of flow will be

`\begin{gathered} V=0.463*0.1667*\sqrt[]{(2*(7120-5340))/(821\lbrack(0.463)^2-(0.1667)^2\rbrack)} \\ =(0.3721m^3)/(s) \end{gathered}`