Question

Please help. I don't understand where to start with this one. If the slope of a strictly decreasing function at the point (a, b) is –4, what is the slope of the inverse of the function at the point (b, a)?

a. -1/4
b. –4
c. –1
d. The slope cannot be determined without knowing the equation of the function.

Answer 1

just assume the equation is y=-4x
to find the inverse you switch x and y so your equation becomes x=-4y, and then solve for y and you get, y=(-1/4)x so the slope is A)-1/4

Answer 2

a.
`-(1)/(4)`

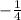
Explanation:

We are given that

Slope of strictly decreasing function at the point (a,b) is -4.

We have to find the slope of the inverse of the function at the point (b,a).

Suppose , we have a function

`y=f(x)=-4x+2`

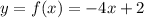
Slope of function f(x) at (x,y)=-4

`-4x=y-2`

`x=-(1)/(4)(y-2)`

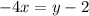
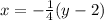
Replace x by y and y by x.

`y=-(1)/(4)(x-2)`

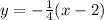
Now, substitute
`y=f^(-1)(x)`

`g(x)=f^(-1)(x)=-(1)/(4)(x-2)`

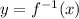
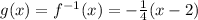
Differentiate w.r.t x

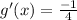`g'(x)=(-1)/(4)` Using rule (
`(dx^n)/(dx)=nx^(n-1)`)

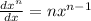Slope of inverse of function f(x) at (y,x)=
`-(1)/(4)`

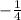
Hence, the slope of inverse of the function at the point (b,a)is
`-(1)/(4)`.

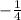Option a is true.