Question

Part b only please if you have time

Answer 1

To convert parametric to Cartesian systems, you need to find a way to get rid of the t's.

In this case, the t's are inside trigonometric functions, so we're going to use a very famous trig identity you should memorize:


`{sin(t)}^(2) + {cos(t)}^(2) = 1`

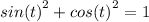
If we plug sin(t) and cos(t) into that equation only x and y variables will be left!

BUT there's one thing. The given cos(t + pi/6) has nasty extra stuff in it. However, part a gives you a tip on how to relate x and y to a nice clean cos(t)

So if we do a little rearranging:


`\sin(t) = (y)/(2) \\ \cos(t) = (x + y)/(2 √(3) )`

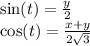
Now we can plug these into the famous trig identity!


`{( (y)/(2)) }^(2) + {( (x + y)/(2 √(3) ) )}^(2) = 1`

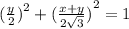
Do a little bit of adjustments to get that final form asked for, and you'll be able to find those integers of a and b. ;)