Intercepts of a Function
There are two possible intercepts for a real function f(x):
* The x-intercepts, if any, are the points where the graph of the function cross the x-axis and can be obtained by setting y=0
* The y-intercepts, if any, are the points where the graph of the function crosses the y-axis and are obtained when x=0.
The function provided is:
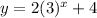
X-intercepts:
Let's make y=0:
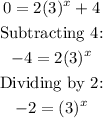
It's not possible to find a value for x that makes an exponential negative, thus there are NO x-intercepts
Y-intercepts:
Now, x=0:
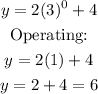
The y-intercept is (0,6), or the point where y=6
-the y-intercept is 6