Question

Which of these statements are true about the intercepts for the graph of the exponential function y=2(3)^x+4? Select all that apply.-the x intercept is 4-the y intercept is 2-the graph has no x intercept-the graph has no y intercept-the x intercept is 0-the x intercept is -2/3-the y intercept is 6 -the y intercept is 4

Answer 1

Intercepts of a Function

There are two possible intercepts for a real function f(x):

* The x-intercepts, if any, are the points where the graph of the function cross the x-axis and can be obtained by setting y=0

* The y-intercepts, if any, are the points where the graph of the function crosses the y-axis and are obtained when x=0.

The function provided is:

`y=2\mleft(3\mright)^x+4`

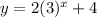
X-intercepts:

Let's make y=0:

`\begin{gathered} 0=2\mleft(3\mright)^x+4 \\ \text{Subtracting 4:} \\ -4=2(3)^x \\ \text{Dividing by 2:} \\ -2=(3)^x \end{gathered}`

It's not possible to find a value for x that makes an exponential negative, thus there are NO x-intercepts

Y-intercepts:

Now, x=0:

`\begin{gathered} y=2(3)^0+4 \\ \text{Operating:} \\ y=2(1)+4 \\ y=2+4=6 \end{gathered}`

The y-intercept is (0,6), or the point where y=6

-the y-intercept is 6