Question

Help, this is after an test. And I still don't understand it. Could someone please help me understand this question related to inverse functions? Thanks! Also: I am supposed to find g(x) as it is the inverse of f(x).

Answer 1

To solve the exercise, we can first find the equation of the line f(x). To do this, we can first take two points through which the line passes and find its slope using this formula:

`\begin{gathered} m=(y_(2)-y_(1))/(x_(2)-x_(1)) \\ \text{ Where m is the slope of the line and} \\ (x_1,y_1)\text{ and }(x_2,y_2)\text{ are two points through which the line passes} \end{gathered}`

In this case, we have:

`\begin{gathered} (x_1,y_1)=(0,2) \\ (x_2,y_2)=(1,0) \\ m=(y_2-y_1)/(x_2-x_1) \\ m=(0-2)/(1-0) \\ m=(-2)/(1) \\ $$\boldsymbol{m=-2}$$ \end{gathered}`

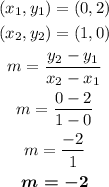
Now we can use the point-slope formula to find the equation of the line f(x):

`\begin{gathered} y-y_1=m(x-x_1) \\ y-2=-2(x-0) \\ y-2=-2(x) \\ y-2=-2x \\ \text{ Add 2 from both sides of the equation} \\ y-2+2=-2x+2 \\ y=-2x+2 \end{gathered}`

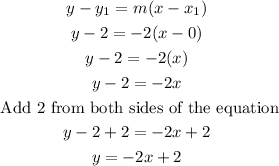
Then, the equation of the line f(x) is:

`\begin{gathered} $$\boldsymbol{f(x)=-2x+2}$$ \\ \text{ or} \\ \boldsymbol{y=-2x+2} \end{gathered}`

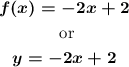
To find the inverse function, g(x), we swap x and y in the equation of the line f(x), solve for y and, we rewrite y as g(x):

`\begin{gathered} y=-2x+2 \\ \text{ Swap x and y} \\ x=-2y+2 \\ \text{ Subtract 2 from both sides of the equation} \\ x-2=-2y+2-2 \\ x-2=-2y \\ \text{ Divide by -2 from both sides of the equation} \\ (x-2)/(-2)=(-2y)/(-2) \\ -(x)/(2)+(-2)/(-2)=y \\ -(x)/(2)+1=y \\ \text{ Rewrite y as g(x)} \\ -(x)/(2)+1=g(x) \end{gathered}`

Then, the equation of the line g(x) is:

`\begin{gathered} \boldsymbol{y=-(x)/(2)+1} \\ \text{ or} \\ \boldsymbol{g(x)=-(x)/(2)+1} \end{gathered}`

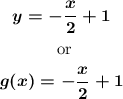
Finally, to complete the table, we can plug the given ordered pair into the equation of the line g(x) and see if the equation is satisfied:

• Ordered pair (-3,4)

`\begin{gathered} x=-3 \\ y=4 \\ y=-(x)/(2)+1 \\ 4\\e-(-3)/(2)+1 \\ 4\\e(3)/(2)+1 \\ 4\\e(3)/(2)+(1)/(1) \\ 4\\e(3\cdot1+2\cdot1)/(2\cdot1) \\ 4\\e(3+2)/(2) \\ 4\\e(5)/(2) \\ 4\\e2.5 \end{gathered}`

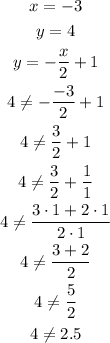
Since 4 is different from 2.5, the ordered pair does not satisfy the equation and therefore is not part of g(x).

• Ordered pair (-2,2)

`\begin{gathered} x=-2 \\ y=2 \\ y=-(x)/(2)+1 \\ 2=-(-2)/(2)+1 \\ 2=(2)/(2)+1 \\ 2=1+1 \\ 2=2 \end{gathered}`

As it is true that 2 is equal to 2, the ordered pair satisfies the equation and, therefore, is part of g(x).

• Ordered pair (4,-1)

`\begin{gathered} x=4 \\ y=-1 \\ y=-(x)/(2)+1 \\ -1=-(4)/(2)+1 \\ -1=-2+1 \\ -1=-1 \end{gathered}`

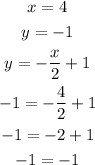
As it is true that -1 is equal to -1, the ordered pair satisfies the equation and, therefore, is part of g(x).

Therefore, the complete table is

You can see the above in the graph shown below: