Question

Determine the end behavior of each function.

(a)    f(x) = 14 + 2x2 − 13x3 − x4
f(x) → as x → −∞
f

Answer 1

This is the function written in descending order of power:

`f(x)=- x^(4) -13 x^(3) +2 x^(2) +14`
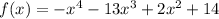
And since the highest power is 4 this function behaves like a quadratic (U-shaped).
If the leading coefficient of the function is positive the graph looks like U but if it is negative it looks like ∩.


`f(x)=<strong>- x^(4)</strong> -13 x^(3) +2 x^(2) +14`
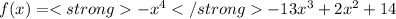
It is negative so the graph is heading towards -∞ on both sides.

`f(x)`→-∞ as x→-∞

Answer 2

Important: express those exponentials using the symbol " ^ ."

Thus:

f(x) = 14 + 2x^2 − 13x^3 − x^4

Then, the limit of f(x) → as x → −∞

is negative infinity. the x^4 term dominates all the other terms, and because x^4 is negative, the final limit will be negative (negative infinity).