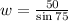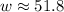To solve for X
X + 90 + 75 = 180° (Sum of interior angle of a triangle)
X + 165 = 180°
Subtract 165 from both-side of the equation
X = 180° - 165°
X = 15°
To solve for x
opposite =50
Adjacent = x
θ=75
Using the trigonometric ratio;
SOH CAH TOA
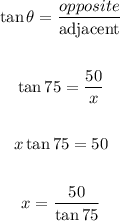
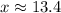
To solve for w,
opposite = 50
hypotenuse= w
θ=75
Hence, we will use sine.
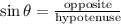
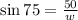
Cross-multiply
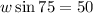
Divide both-side by sin75