Question

PLS HELP I NEED A COMPLETE ANSWER AND PROCEDURE FOR THIS, IT'S TIMED

A motorcyclist heading east through a small town accelerates at a constant 4.0 m/s² after he leaves the city limits. At time t=0 he is 5.0 m east of the city-limits signpost while he moves east at 15 m/s. Where is he when his speed is 25 m/s?

Answer 1

The motorcyclist is 55 miles east of the small town.

Step-by-step explanation:

Motion With Constant Acceleration

It's a type of motion where the velocity of an object changes uniformly in time.

The equation that rules the change of velocities is:

`v_f=v_o+at\qquad\qquad [1]`

Where:

a = acceleration

vo = initial speed

vf = final speed

t = time

The distance traveled by the object is given by:

`\displaystyle x=v_o.t+(a.t^2)/(2)\qquad\qquad [2]`

Using the equation [1] we can solve for a:

`\displaystyle a=(v_f-v_o)/(t)`

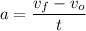
Solving [1] for t and substituting into [2] we get the following equation:

`V_f^2=V_o^2+2aX`

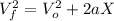
The motorcyclist has an acceleration of a=4\ m/s^2 and an initial distance of 5 m where he travels at vo=15 m/s. It's required to calculate the distance when the speed is vf=25 m/s.

Solving the last equation for X:

`\displaystyle X=(V_f^2-V_o^2)/(2a)`

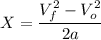
Substituting:

`\displaystyle X=(25^2-15^2)/(2*4)`

`\displaystyle X=(625-225)/(8)`

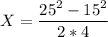
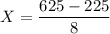
X = 50 m

Adding the initial distance:

The motorcyclist is 55 miles east of the small town.