Question

Select Linear or Nonlinear for each function. Function Linear Nonlinear y = 15 y=3−x3 y = 11 + 5x

Answer 1

Linear functions are represented by straight lines, while nonlinear functions have curved graphs.

Step-by-step explanation:

Linear: A linear function is a function whose graph is a straight line. It can be represented by an equation in the form y = mx + b, where m is the slope and b is the y-intercept. Examples of linear functions are y = 15 and y = 11 + 5x.

Nonlinear: A nonlinear function is a function whose graph is not a straight line. It cannot be represented by an equation in the form y = mx + b. An example of a nonlinear function is y = 3 - x^3.

Answer 2

We have these three functions:
y=15

`y=3-x^3`
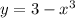
y=11+5x

First, let's look at y=15.
If you graph this, this is just a horizontal line with a y value of 15.
Thus, the first function is linear.

Next, let's look at
`y=3-x^3`
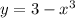
Notice that this function has an x to a power of 3.
Since this power is greater than 1, this cannot be linear.
Thus, the second function is nonlinear.

Finally, let's look at y=11+5x.
Let's change the order of the 11 and 5x.
We get y=5x+11.
This function is in the form of y=mx+b, which is the slope-intercept form of a line (where m is the slope and b is the y-intercept).
Thus, the last function is linear.

Have an awesome day/night!

~collinjun0827, Junior Moderator