Question

4. Suppose the spread of disease can be modeled using an exponential function. Let x refer to the number ofdays that have gone by, and f(x) represent the number of people who are infected.(a) If 9 people are initially infected and the number of infected people increase by 40% per day(transmission rate), write down the associated exponential function.(b) Using the function you wrote in Question 4a, how many people are infected after 30 days? Roundto the nearest whole number.(c) If 9 people are initially infected and the number of infected people increase by 21% per day (transmissionrate), write down the associated exponential function.(D) using the function you wrote in Question 4c, how many people are infected after 30 days? Round to the nearest whole number. (E) what does it mean when the transmission rate is lower based on your results from parts (a) through (d)? Hint compare the results and write a sentence with your conclusion

Answer 1

• (a)f(x)=9(1.4)^x

,

• (b)217,813 people

,

• (c)f(x)=9(1.21)^x

,

• (d)2740 people

Step-by-step explanation:

• Let x refer to the number of days that have gone by

,

• f(x) represents the number of people who are infected.

Part A

• Initial Number of Infected = 9

,

• Rate of increase = 40% per day

The associated exponential function is derived below:

`\begin{gathered} f(x)=f(0)_{}(1+r)^x \\ f(x)=9(1+0.4)^x \\ \implies f(x)=9(1.4)^x \end{gathered}`

Part B

After 30 days i,e when x=30

`\begin{gathered} f(x)=9(1.4)^(30) \\ =217812.9 \\ \approx217,813\text{ people} \end{gathered}`

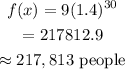
Part C

• Initial Number of Infected = 9

,

• Rate of increase = 21% per day

The associated exponential function is derived below:

`\begin{gathered} f(x)=f(0)_{}(1+r)^x \\ f(x)=9(1+0.21)^x \\ \implies f(x)=9(1.21)^x \end{gathered}`

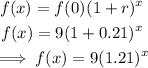
Part D

After 30 days i,e when x=30

`\begin{gathered} f(x)=9(1.21)^(30) \\ =2740.3 \\ \approx2740\text{ people} \end{gathered}`

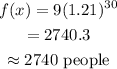
Part E

When the transmission rate is lower (21%), the number of infected (2,740 infected) after 30 days will be less than the number of infected(217,813) when the transmission rate is higher(40%).