Question

In some year, a candy shop produced 100 boxes of candy per working day in January. In each month following this, the shop produced 25 more boxes of candy per working day in addition to the previous month.

a) How many boxes did the candy shop produce on each working day in October?

b)How many boxes did the candy shop produce in that year, assuming that each month has 20 working days?

Answer 1

A: The shop made 6500 boxes of candy in the month of October.

B: Assuming the shop works 20 days per month it made 57,000 boxes of candy in that one year if they made candy boxes according to each month on every work day.

Answer 2

a). 325 boxes per day

b). 717000 boxes

Explanation:

A candy shop produced 100 boxes of candies per working day in January.

From the next month shop produced 25 more boxes of candies per working day from the next month.

So the sequence formed for each month will be,

100, 125, 150, 175........

This sequence has a common difference 'd' = 125 - 100 = 25, in every subsequent month.

Therefore, it's an arithmetic progression.

First term of the sequence is 'a' = 100.

Explicit formula for the nth term of this sequence is

`T_(n)=a+(n-1)d`

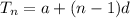
where a = first term

and d = common difference

n = number of term

a). For October means n = 10, productivity will be

`T_(10)=100+(10-1)(25)`

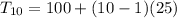
= 100 + 225

= 325 boxes per day

b). If working days in a month are 20 then number of boxes produced in every month will be

2000, 12500, 15000........

So the sequence has first term 'a' = 2000

Common difference 'd' = 12500 - 2000 = 10500

Sum of the sequence for 12 terms, 'n' = 12

Total boxes produced =
`(n)/(2)[2a+(n-1)d]`

=
`(12)/(2)[(2* 2000)+(12-1)10500]`

= 6[4000 + 115500]

= 717000 boxes